Publications
8. Electrohydrodynamic drift of a drop away from an insulating wall
D. Sen, M. Firouznia, J. A. Koch, D. Saintillan, P. M. Vlahovska, arXiv:2504.17257 (2025).
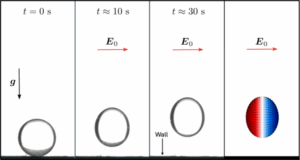 An isolated charge-neutral drop suspended in an unbounded medium does not migrate in a uniform DC electric field. A nearby wall breaks the symmetry and causes the drop to drift towards or away from the boundary, depending on the electric properties of the fluids and the wall. In the case of an electrically insulating wall and an electric field applied tangentially to the wall, the interaction of the drop with its electrostatic image gives rise to repulsion by the wall. However, the electrohydrodynamic flow causes either repulsion for a drop with R/P<1, where R and P are the drop-to-medium ratios of conductivity and permittivity, respectively, or attraction for R/P>1. We experimentally measure droplet trajectories and quantify the wall-induced electrohydrodynamic lift in the case R/P<1. Numerical simulations using the boundary integral method agree well with the experiment and also explore the R/P>1 case. The results show that the lateral migration of a drop in a uniform electric field applied parallel to an insulating wall is dominated by the long-range flow due to the image stresslet.
An isolated charge-neutral drop suspended in an unbounded medium does not migrate in a uniform DC electric field. A nearby wall breaks the symmetry and causes the drop to drift towards or away from the boundary, depending on the electric properties of the fluids and the wall. In the case of an electrically insulating wall and an electric field applied tangentially to the wall, the interaction of the drop with its electrostatic image gives rise to repulsion by the wall. However, the electrohydrodynamic flow causes either repulsion for a drop with R/P<1, where R and P are the drop-to-medium ratios of conductivity and permittivity, respectively, or attraction for R/P>1. We experimentally measure droplet trajectories and quantify the wall-induced electrohydrodynamic lift in the case R/P<1. Numerical simulations using the boundary integral method agree well with the experiment and also explore the R/P>1 case. The results show that the lateral migration of a drop in a uniform electric field applied parallel to an insulating wall is dominated by the long-range flow due to the image stresslet.
7. Self-organized dynamics of a viscous drop with interfacial nematic activity
M. Firouznia, D. Saintillan, Physical Review Research, 7 L012054 (2025).
 We study emergent dynamics in a viscous drop subject to interfacial nematic activity. Using hydrodynamic simulations, we show how the interplay of nematodynamics, activity-driven flows and surface deformations gives rise to a sequence of self-organized behaviors of increasing complexity, from periodic braiding motions of topological defects to chaotic defect dynamics and active turbulence, along with spontaneous shape changes and translation. Our findings recapitulate qualitative features of experiments and shed light on the mechanisms underpinning morphological dynamics in active interfaces.
We study emergent dynamics in a viscous drop subject to interfacial nematic activity. Using hydrodynamic simulations, we show how the interplay of nematodynamics, activity-driven flows and surface deformations gives rise to a sequence of self-organized behaviors of increasing complexity, from periodic braiding motions of topological defects to chaotic defect dynamics and active turbulence, along with spontaneous shape changes and translation. Our findings recapitulate qualitative features of experiments and shed light on the mechanisms underpinning morphological dynamics in active interfaces.
6. A spectral boundary integral method for simulating electrohydrodynamic flows in viscous drops
M. Firouznia, S. H. Bryngelson, D. Saintillan, Journal of Computational Physics, 112248 (2023).
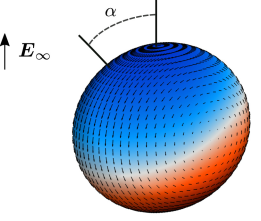 A weakly conducting liquid droplet immersed in another leaky dielectric liquid can exhibit rich dynamical behaviors under the effect of an applied electric field. Depending on material properties and field strength, the nonlinear coupling of interfacial charge transport and fluid flow can trigger electrohydrodynamic instabilities that lead to shape deformations and complex dynamics. We present a spectral boundary integral method to simulate droplet electrohydrodynamics in a uniform electric field. All physical variables, such as drop shape and interfacial charge density, are represented using spherical harmonic expansions. In addition to its exponential accuracy, the spectral representation affords a nondissipative dealiasing method required for numerical stability. A comprehensive charge transport model, valid under a wide range of electric field strengths, accounts for charge relaxation, Ohmic conduction, and surface charge convection by the flow. A shape reparametrization technique enables the exploration of significant droplet deformation regimes. For low-viscosity drops, the convection by the flow drives steep interfacial charge gradients near the drop equator. This introduces numerical ringing artifacts we treat via a weighted spherical harmonic expansion, resulting in solution convergence. The method and simulations are validated against experimental data and analytical predictions in the axisymmetric Taylor and Quincke electrorotation regimes.
A weakly conducting liquid droplet immersed in another leaky dielectric liquid can exhibit rich dynamical behaviors under the effect of an applied electric field. Depending on material properties and field strength, the nonlinear coupling of interfacial charge transport and fluid flow can trigger electrohydrodynamic instabilities that lead to shape deformations and complex dynamics. We present a spectral boundary integral method to simulate droplet electrohydrodynamics in a uniform electric field. All physical variables, such as drop shape and interfacial charge density, are represented using spherical harmonic expansions. In addition to its exponential accuracy, the spectral representation affords a nondissipative dealiasing method required for numerical stability. A comprehensive charge transport model, valid under a wide range of electric field strengths, accounts for charge relaxation, Ohmic conduction, and surface charge convection by the flow. A shape reparametrization technique enables the exploration of significant droplet deformation regimes. For low-viscosity drops, the convection by the flow drives steep interfacial charge gradients near the drop equator. This introduces numerical ringing artifacts we treat via a weighted spherical harmonic expansion, resulting in solution convergence. The method and simulations are validated against experimental data and analytical predictions in the axisymmetric Taylor and Quincke electrorotation regimes.
5. Instability of a planar fluid interface under a tangential electric field in a stagnation point flow
M. Firouznia, M. J. Miksis, P. M. Vlahovska, D. Saintillan, Journal of Fluid Mechanics, 931 A25 (2022).
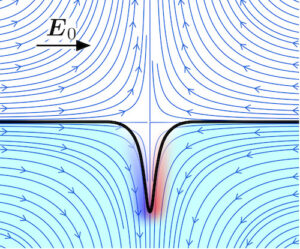 The interface between two immiscible fluids can become unstable under the effect of an imposed tangential electric field along with a stagnation point flow. This canonical situation, which arises in a wide range of electrohydrodynamic systems including at the equator of electrified droplets, can result in unstable interface deflections where the perturbed interface gets drawn along the extensional axis of the flow while experiencing strong charge build-up. Here, we present analytical and numerical analyses of the stability of a planar interface separating two immiscible fluid layers subject to a tangential electric field and a stagnation point flow. The interfacial charge dynamics is captured by a conservation equation accounting for Ohmic conduction, advection by the flow and finite charge relaxation. Using this model, we perform a local linear stability analysis in the vicinity of the stagnation point to study the behavior of the system in terms of the relevant dimensionless groups of the problem. The local theory is complemented with a numerical normal-mode linear stability analysis based on the full system of equations and boundary conditions using the boundary element method. Our analysis demonstrates the subtle interplay of charge convection and conduction on the dynamics of the system, which oppose one another in the dominant unstable eigenmode. Finally, numerical simulations of the full nonlinear problem demonstrate how the coupling of flow and interfacial charge dynamics can give rise to nonlinear phenomena such as tip formation and the growth of charge density shocks.
The interface between two immiscible fluids can become unstable under the effect of an imposed tangential electric field along with a stagnation point flow. This canonical situation, which arises in a wide range of electrohydrodynamic systems including at the equator of electrified droplets, can result in unstable interface deflections where the perturbed interface gets drawn along the extensional axis of the flow while experiencing strong charge build-up. Here, we present analytical and numerical analyses of the stability of a planar interface separating two immiscible fluid layers subject to a tangential electric field and a stagnation point flow. The interfacial charge dynamics is captured by a conservation equation accounting for Ohmic conduction, advection by the flow and finite charge relaxation. Using this model, we perform a local linear stability analysis in the vicinity of the stagnation point to study the behavior of the system in terms of the relevant dimensionless groups of the problem. The local theory is complemented with a numerical normal-mode linear stability analysis based on the full system of equations and boundary conditions using the boundary element method. Our analysis demonstrates the subtle interplay of charge convection and conduction on the dynamics of the system, which oppose one another in the dominant unstable eigenmode. Finally, numerical simulations of the full nonlinear problem demonstrate how the coupling of flow and interfacial charge dynamics can give rise to nonlinear phenomena such as tip formation and the growth of charge density shocks.
4. Electrohydrodynamic instabilities in freely suspended viscous films under normal electric fields
M. Firouznia, D. Saintillan, Physical Review Fluids, 6 103703 (2021).
Electrohydrodynamic instabilities of fluid-fluid interfaces can be exploited in various microfluidic applications in order to enhance mixing, replicate well-controlled patterns or generate drops of a particular size. In this work, we study the stability and dynamics of a system of three superimposed layers of two immiscible fluids subject to a normal electric field. Following the Taylor-Melcher leaky dielectric model, the bulk remains electroneutral while a net charge accumulates on the interfaces. The interfacial charge dynamics is captured by a conservation equation accounting for Ohmic conduction, advection by the flow and finite charge relaxation. Using this model, we perform a linear stability analysis and identify different modes of instability, and we characterize the behavior of the system as a function of the relevant dimensionless groups in each mode. Further, we perform numerical simulations using the boundary element method in order to study the effect of nonlinearities on long-time interfacial dynamics. We demonstrate how the coupling of flow and surface charge transport in different modes of instability can give rise to nonlinear phenomena such as tip streaming or pinching of the film into droplets.
3. Shear-induced migration and axial development of particles in channel flows of non-Brownian suspensions
A. Rashedi, M. Sarabian, M. Firouznia, D. Roberts, G. Ovarlez, S. Hormozi, AIChE Journal, 66(12), e17100 (2020).
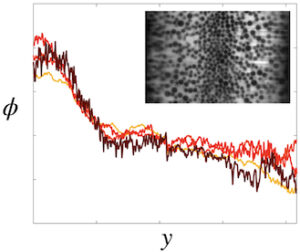 We present an experimental study on the shear‐induced migration and axial development of particles in the channel flows of non‐Brownian suspensions. The suspending fluid is Newtonian. We investigate fracturing flows with a Hele‐Shaw type scaling through building a unique channel setup and an advanced optical system. The local particle concentration profiles are measured via the refractive‐index matching technique for a wide range of bulk volume fractions. Simultaneously, the particle image velocimetry is performed to determine the velocity profile of the particle phase. We compare our experimental results with the available two‐phase continuum frameworks and show discrepancies and similarities in the fully developed and axial development of the solid volume fraction profiles. We discuss directions in which the continuum frameworks require improvements.
We present an experimental study on the shear‐induced migration and axial development of particles in the channel flows of non‐Brownian suspensions. The suspending fluid is Newtonian. We investigate fracturing flows with a Hele‐Shaw type scaling through building a unique channel setup and an advanced optical system. The local particle concentration profiles are measured via the refractive‐index matching technique for a wide range of bulk volume fractions. Simultaneously, the particle image velocimetry is performed to determine the velocity profile of the particle phase. We compare our experimental results with the available two‐phase continuum frameworks and show discrepancies and similarities in the fully developed and axial development of the solid volume fraction profiles. We discuss directions in which the continuum frameworks require improvements.
2. Fully developed and transient concentration profiles of particulate suspensions sheared in a cylindrical Couette cell
M. Sarabian, M. Firouznia, B. Metzger, S. Hormozi, Journal of Fluid Mechanics, 862 659-671 (2019).
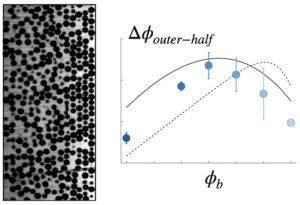 We experimentally investigate particle migration in a non-Brownian suspension sheared in a Taylor–Couette configuration and in the limit of vanishing Reynolds number. Highly resolved index-matching techniques are used to measure the local particulate volume fraction. In this wide-gap Taylor–Couette configuration, we find that for a large range of bulk volume fraction, [20%−50%], the fully developed concentration profiles are well predicted by the suspension balance model of Nott & Brady 1994. Moreover, we provide systematic measurements of the migration strain scale and of the migration amplitude which highlight the limits of the suspension balance model predictions.
We experimentally investigate particle migration in a non-Brownian suspension sheared in a Taylor–Couette configuration and in the limit of vanishing Reynolds number. Highly resolved index-matching techniques are used to measure the local particulate volume fraction. In this wide-gap Taylor–Couette configuration, we find that for a large range of bulk volume fraction, [20%−50%], the fully developed concentration profiles are well predicted by the suspension balance model of Nott & Brady 1994. Moreover, we provide systematic measurements of the migration strain scale and of the migration amplitude which highlight the limits of the suspension balance model predictions.
1. The interaction of two spherical particles in simple-shear flows of yield stress fluids
M. Firouznia, B. Metzger, G. Ovarlez, S. Hormozi, Journal of Non-Newtonian Fluid Mechanics, 255 19-38 (2018).
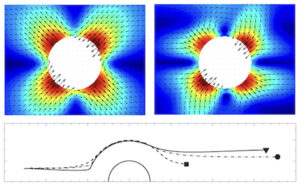 This study focuses on the interaction of two small freely-moving spheres in a linear flow field of yield stress fluids. We perform a series of experiments over a range of shear rates and different shear histories using an original apparatus and with the aid of conventional rheometry, Particle Image Velocimetry (PIV), and Particle Tracking Velocimetry (PTV). We investigate the flow field around a single sphere as well as two spheres in a simple-shear flow. The flow is Stokesian and the Bingham number is in the range of 0 ≤ B ≤ 2. To explore the limit of zero Bingham number, we use both Newtonian and shear-thinning suspending fluids. We use guar gum solutions and Carbopol gels as shear thinning and yield stress test fluids, respectively. We show that the presence of a slight elasticity, which is unavoidable when dealing with polymer solutions, plays an important role in establishing the flow field, e.g., disturbance velocities and streamlines around a single sphere as well as particle trajectories. Therefore, ideal yield stress fluid models cannot provide a full description of flow problems involving particles in practical yield stress fluids. The flow field around a single sphere can be used to understand the two-particle interactions. We show how particle-particle contact and non-Newtonian behaviors result in relative trajectories with fore-aft asymmetry. Particularly, the fore-aft asymmetry depends on the Deborah number, Bingham number, shear history, initial offset, and roughness of the particles. Finally, we discuss how the relative particle trajectories may affect the microstructure of complex suspensions and consequently the bulk rheology.
This study focuses on the interaction of two small freely-moving spheres in a linear flow field of yield stress fluids. We perform a series of experiments over a range of shear rates and different shear histories using an original apparatus and with the aid of conventional rheometry, Particle Image Velocimetry (PIV), and Particle Tracking Velocimetry (PTV). We investigate the flow field around a single sphere as well as two spheres in a simple-shear flow. The flow is Stokesian and the Bingham number is in the range of 0 ≤ B ≤ 2. To explore the limit of zero Bingham number, we use both Newtonian and shear-thinning suspending fluids. We use guar gum solutions and Carbopol gels as shear thinning and yield stress test fluids, respectively. We show that the presence of a slight elasticity, which is unavoidable when dealing with polymer solutions, plays an important role in establishing the flow field, e.g., disturbance velocities and streamlines around a single sphere as well as particle trajectories. Therefore, ideal yield stress fluid models cannot provide a full description of flow problems involving particles in practical yield stress fluids. The flow field around a single sphere can be used to understand the two-particle interactions. We show how particle-particle contact and non-Newtonian behaviors result in relative trajectories with fore-aft asymmetry. Particularly, the fore-aft asymmetry depends on the Deborah number, Bingham number, shear history, initial offset, and roughness of the particles. Finally, we discuss how the relative particle trajectories may affect the microstructure of complex suspensions and consequently the bulk rheology.